密码学

第一章

发展概况

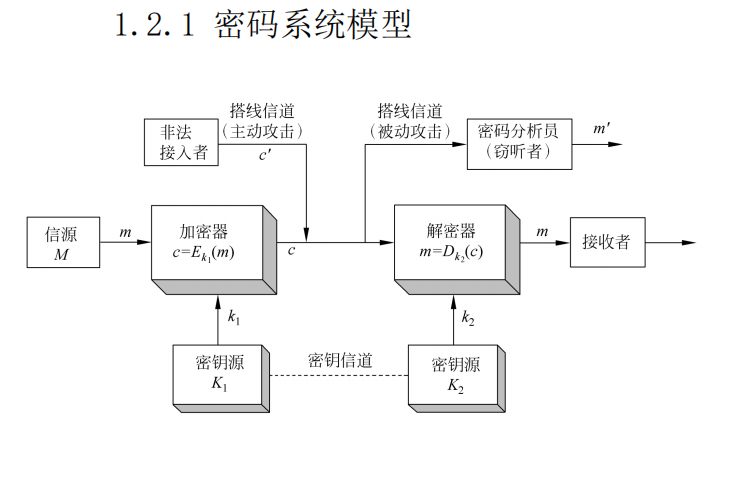
• 消息（明文）->密文->明文

• 加密过程：$E_k(M) = C$

• 解密过程：$D_k(C) = M$

• 如果是非对称加密，则有：

  • $E_{k1}(M) = C$
  • $D_{k2}(C) = M$

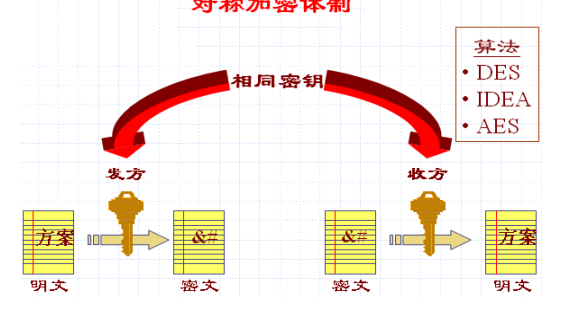
• 对称算法（单钥算法）：

  ​

• 非对称算法：

  ​​

基础概念：

​​

密码体制分类：

• 对称密码（单钥密码，私钥密码）：加密密钥和解密的一样

  • 如：分组密码，流密码

• 非对称密码（公钥密码，双钥密码）：加密密钥和解密密钥不同

  • 如：公钥密码

• 好的密码体制要求：

  1. 容易计算出密文，和恢复明文
  2. 在不知道解密密钥$k_2$时，不可能从密文$c$恢复出明文$m$

• 可破译的：可以根据密文得到明文或者密钥，或根据明文及对应的密文确定密钥

攻击方法：

• 攻击密码体制的方法

  • 穷举攻击
  • 统计分析攻击
  • 解密变换攻击

• 可以在下列情况下进行攻击：

  • 唯密文攻击
  • 已知明文攻击
  • 选择明文攻击
  • 选择密文攻击

• 密码算法只要满足一下两条准则之一即可（如果两个都满足，那么这个密码算法在实际上是可以使用的）：

  • 破译密码的代价 > 密文价值
  • 破译密码的时间 > 密文有用期

古典密码体制

置换密码

• 概念：明文中的字发生了重新排列，即位置发生改变（注意！字的本身不发生改变）

• 例如：报文倒置（按字的顺序依次倒置）

  ​​

单表代替密码

• 代替密码：每一个字都替换成另一个字符

1. 加法密码

   $f(a_i) = a_j,j = i+k \pmod n$​

   • 例如$k=3$时，$abc \to def$

2. 乘法密码

   $f(a_i) = a_j,j = ik \pmod n,((k,n) = 1)$

   • 例如$k=3$时，$abc\to cfi$

3. 仿射密码（加法和乘法的结合）

   $f(a_i) = a_j,j = k_0+ik_1 \pmod n,((k_1,n) = 1)$

   • 例如$k_0=1,k_1=3$时，$abc \to dgj$

4. 密钥短语代替密码

   • 首先选用一个单词串作为密钥，称为密钥短语
   • 例如HELLO，去掉其中重复的字符得到一个无重复字母的字母串，HELO，然后密码表中如下：

     a	b	c	d	e	f	…
     H	E	L	O	A	B	…

多表代换密码

• 将明文$M$分为由$n$个字母构成的分组$M_1,…,M_k$，对每个分母$M_i$的加密为：$C_i \equiv AM_i+B \pmod N$

  其中$(A,B)$是密钥，$A是n*n$的可逆矩阵，满足$gcd(|A|,N) = 1$

• ​

• ​​

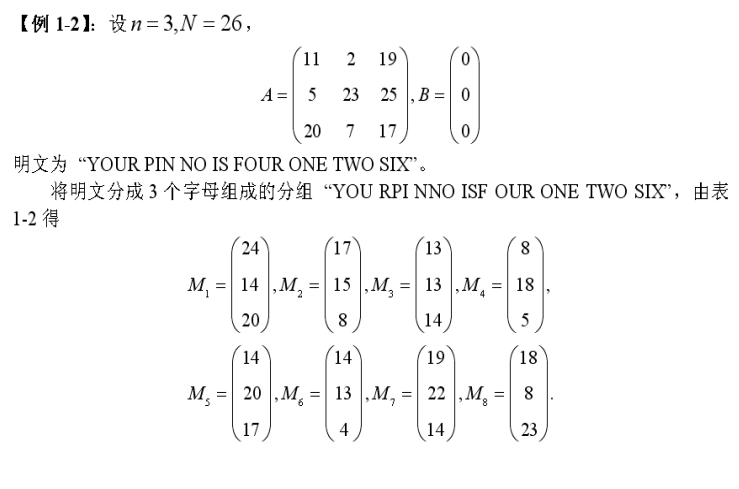
第二章

• 流密码的处理对象是比特，而不是字母

  • $c_i = p_i \oplus k_i \to p_i = c_i \oplus k_i$

  • 密码是循环使用的，但是周期很大

• 一次一密体系：

  • 当随机密钥和明文等长时，唯一可理论证明是无条件安全的
  • 但是难以实现，因为难以产生大量真随机密钥，难以及时安全的发放大量密钥

• 无条件安全：

  • 需要满足：一次一密；明密等长；随机密钥
  • ‍

流密码的基本概念：

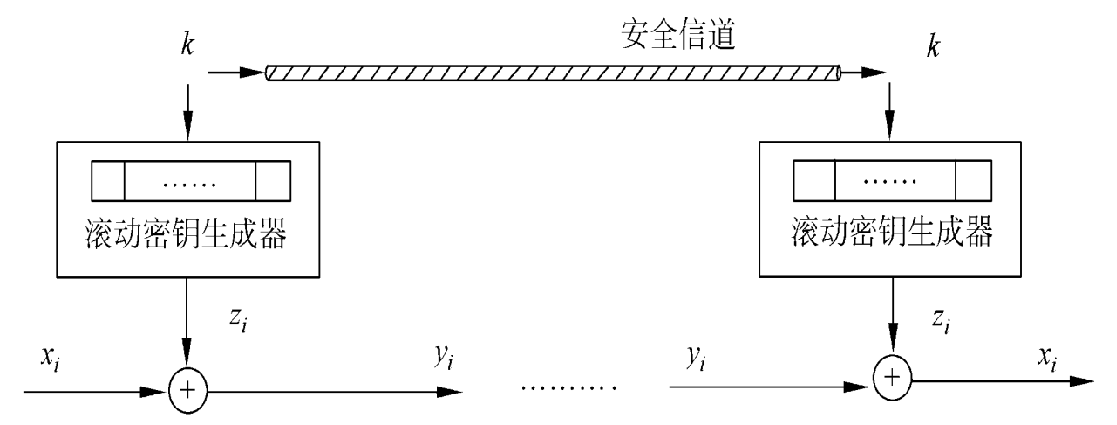
• 明文 $x = x_0x_1x_2…$

  密钥 $z = z_0z_1z_2…$

  密文 $y = y_0y_1y_2…$

  加密变换 $y_i = x_i \oplus z_i$

  解密变换 $x_i = y_i \oplus z_i$

  ​​

线性反馈移位寄存器：

​​

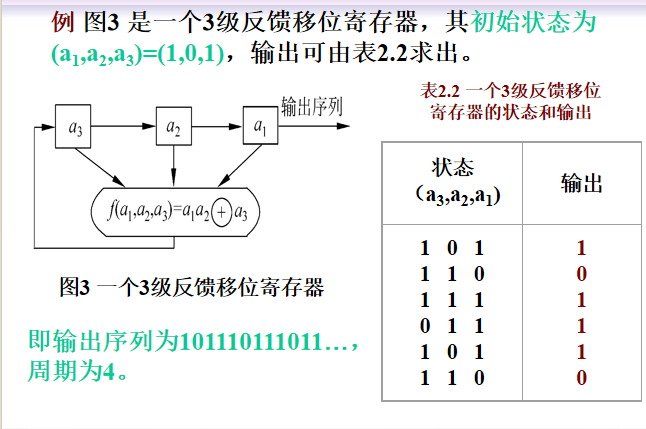
• 需要注意，输出是$a_1$，而不是计算出来的结果

​​

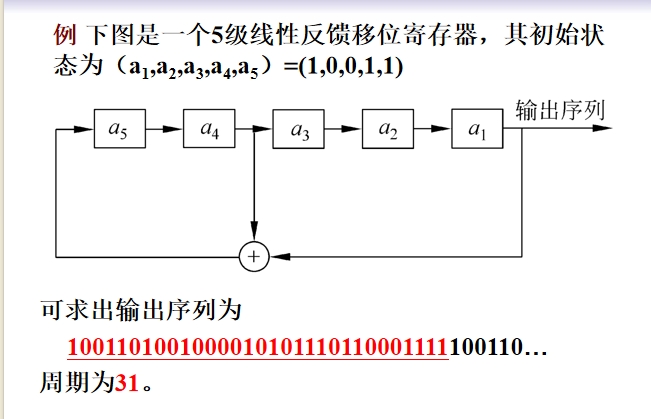
• 哪一些连接了加号，就说明函数中有这些，$f = a_1 \oplus a_4$
• 如果周期为$2^n - 1$（$n$是变量的个数）就说明它的周期达到了最大值，是m序列

第三章

分组密码基本的代换-置换结构

• 分组密码：明文流被划分为 等长串 ，各串用 相同的加密算法和相同的密钥 加密

• 构造原则：

  • 足够大的分组长度（明文空间大，避免给攻击者提供太多的明文统计特征信息）
  • 密钥空间大（防止密钥穷举攻击）
  • 保证足够强的密码算法复杂度以加强分组密码算法自身的安全性。
  • 软件实现尽量采用子块以及加法、乘法、异或和移位等简单运算指令，易于标准处理器完成运算
  • 加解密硬件结构最好一致，便于应用超大规模集成芯片实现，以简化系统整体结构的复杂性。

  采用最多的是S-P网络

  ​

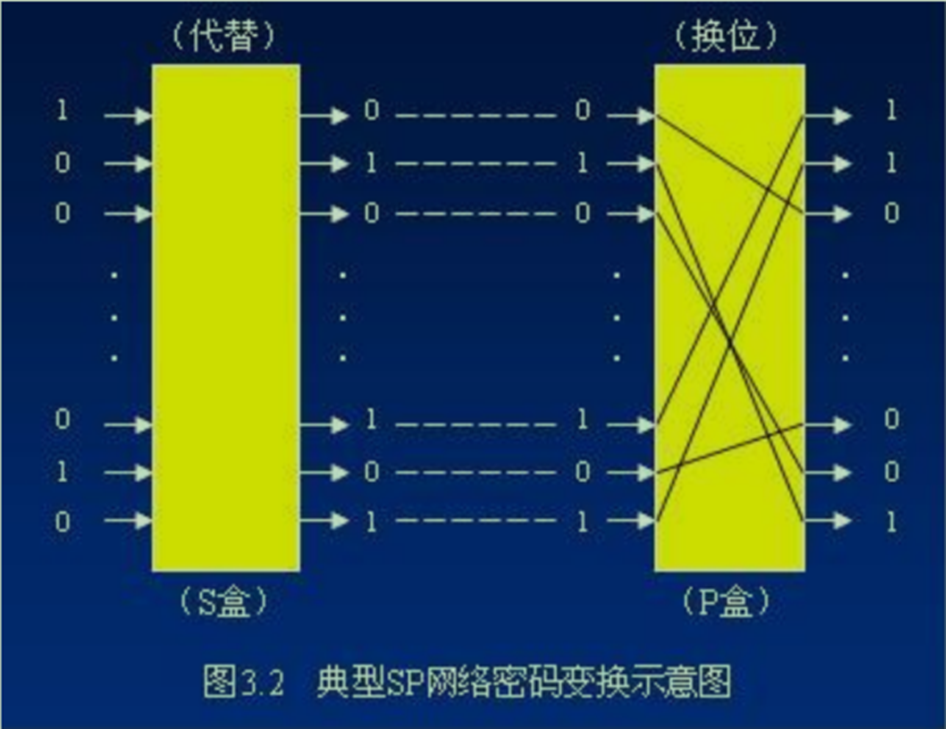
• 完美安全的分组映射：允许生成最大数量的加密映射来映射明文分组

  • $n$位的分组就有 $2^n$种输入
  • 每种输入需要$n$位密钥控制，所以总共需要$n2^n$位密钥

  ​​

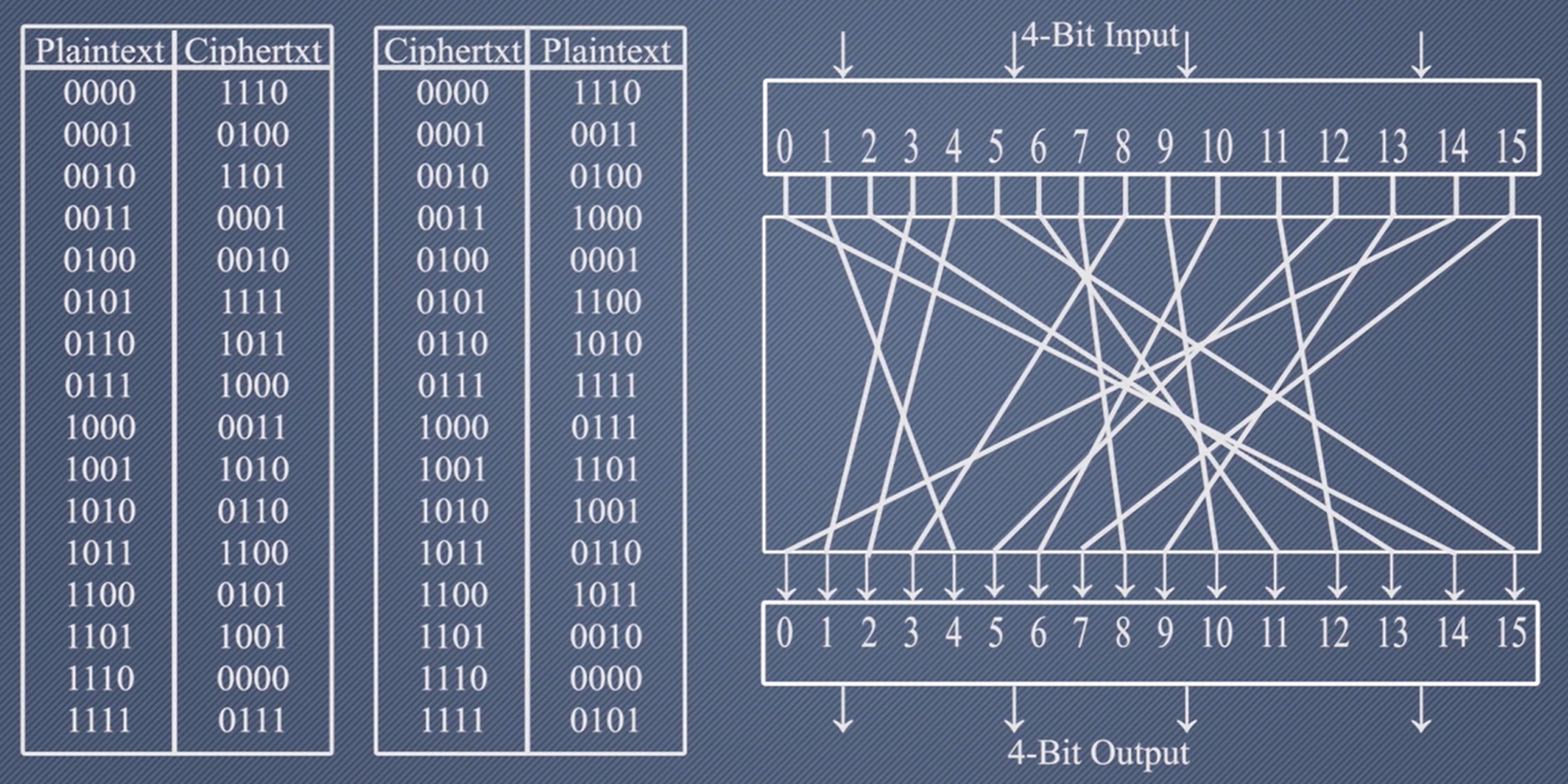
分组密码的原理与设计准则

• SP置换网络

  • S变换：把输入的一个n长的比特串转化为另一个m长的比特串输出，起到 混乱 的效果。
  • P变换：通过把一个比特串中各比特的位置次序重新排列而得到新的比特串的变换，起到 扩散 的效果。
  • 混乱：是指明文与密钥、以及密文之间的统计关系尽可能复杂化，使破译者无法理出相互间的依赖关系，从而加强隐蔽性。采用复杂的非线性代替变换(比如S盒单元)就可达到比较好的混乱效果。
  • 扩散：是指让明文中的每一位(包括密钥的每一位)直接或间接影响输出密文中的许多位，或者让密文中的每一位受制于输入明文以及密钥中的若干位，以便达到隐蔽明文的统计特性。它强调输入位只要很小变化，经过多轮变换后将导致输出发生多位变化，即明文的每位比特变化将引起密文许多比特位迅速发生改变。

• Feistel密码框架

  ​​

  • 加密算法：

    • 将输入等分为两段，然后根据上面规则进行运算

      • 每一轮：对左半段数据进行代换，根据轮函数F（右半段数据，Ki）。然后左右置换

  • 解密算法：

    • 和加密算法过程一致，只不过子密钥使用次序相反

  • 正确性证明：

    ​​

  • 注意轮函数F不需要满足任何单射条件，因为一个Feistel型轮函数必定可逆

• 设计准则需要考虑：

  • S盒设计：加密算法的混淆作用，直接影响整个分组密码算法的安全强度。

    • 非线性度。目前采用的是群加密运算乘法$\pmod {2^n +1 }$
    • 差分均匀性。抵抗差分密码分析的能力要强。
    • 雪崩效应。这与P盒的功能有关，是混淆—扩散特性的进一步反映，要求有良好的雪崩效果，即要求当输入有一比特发生变化时，将导致输出有一半的比特位发生变化。
    • 可逆性、没有“陷门”

  • P盒设计

    • 由于P盒多半是继若干个S盒部件之后，因此，P盒的设计准则就是要实现良好的雪崩效应,进一步增加扩散程度。 比如DES中要求1比特输入希望能引起大约一半输出位的快速变化响应

  • 轮函数F的设计：轮函数F通常是指迭代分组密码中单轮加密算法的非线性函数。

    • 安全性：轮函数F必须能抵抗所有已知的密码攻击方法，尤其是抵抗差分密码分析和线性密码分析。
    • 速度
    • 灵活性：支持密码算法能在多平台和多处理器上实现

  • 迭代轮数：

    • 一般来说越多越好，但是太多了设计很复杂。一般采用r=8,10,12,16,20的居多。
    • 准则是：使密码分析的难度大于简单穷举攻击的难度。

  • 密钥扩展算法：是从初始（种子）密钥产生迭代各轮要使用的子密钥的算法

    • 结构简单，便于实现
    • 至少应保证密钥和密文符合​** 位独立准则 ​和​ 严格雪崩效应准则 **​ ；
    • 不存在简单数学关系,获取前后的位比特联系在计算上是困难的
    • 没有弱密钥（弱密钥通常是指因设计不当或不可避免存在的会明显降低密码算法安全性的一类密钥）
    • 保证种子密钥的各比特对每个子密钥比特影响的均衡性
    • 速度

数据加密标准DES密码算法

​​

​​

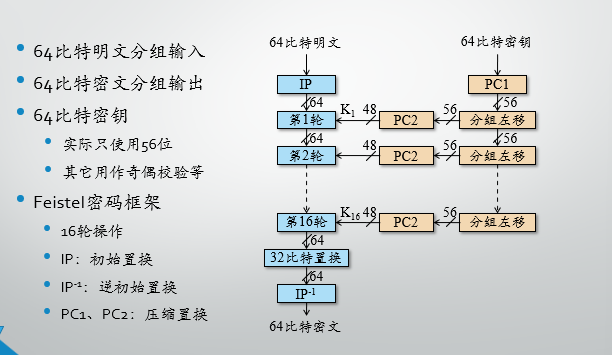
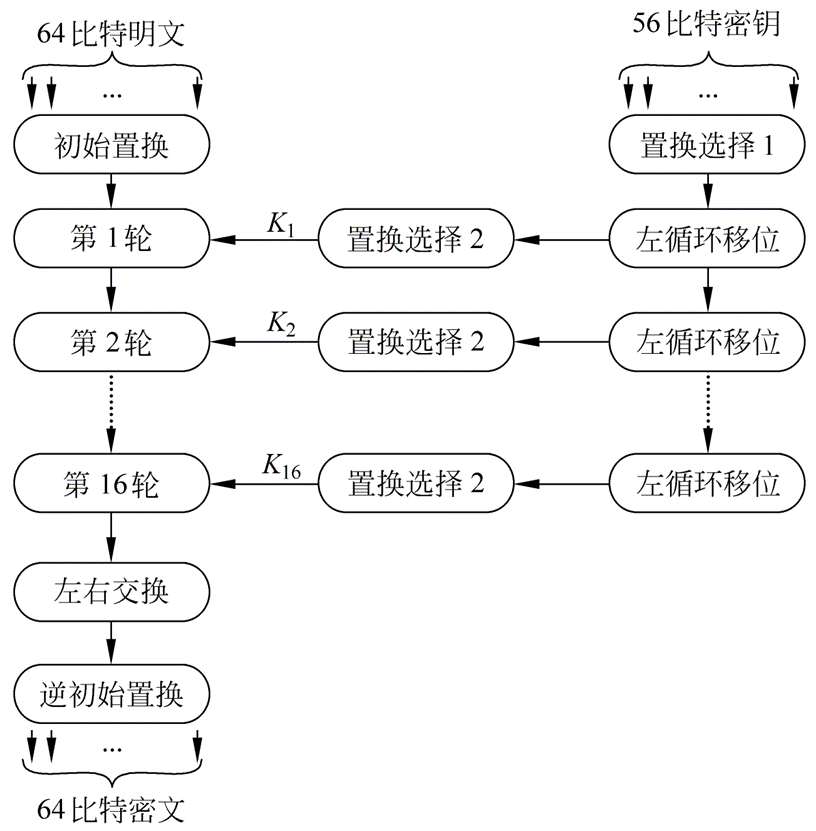
• 在进行16轮加密前，明文会有一个初始置换IP，写作$IP(x) = L^0R^0$，最后16轮加密后，做一次逆置换$y=IP^{-1}(R^{16}L^{16})$

• 初始置换：

  ​​

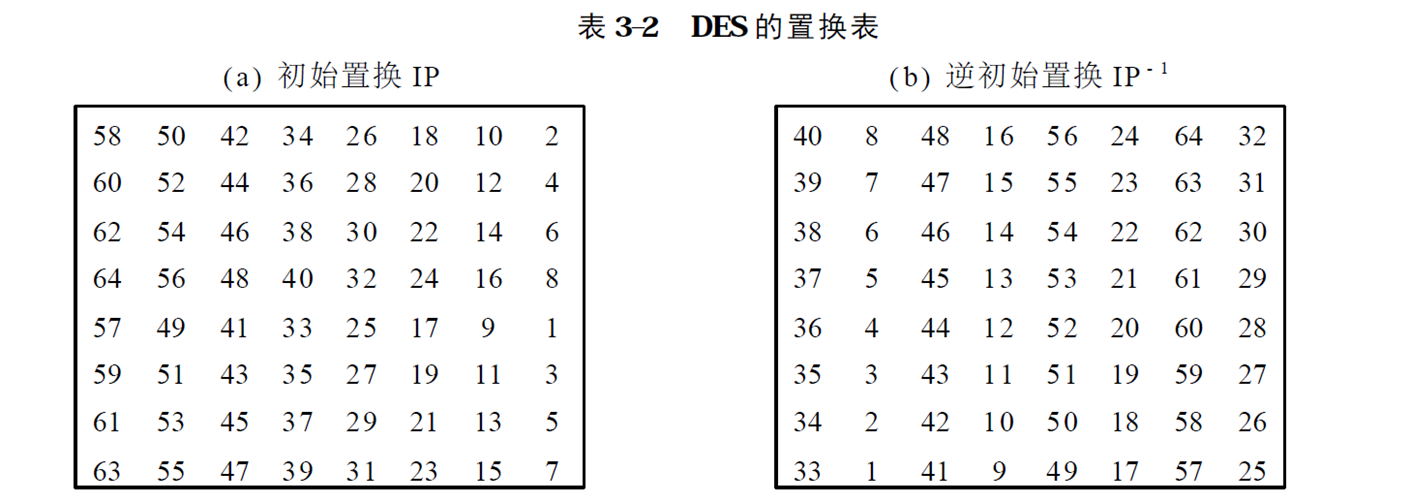
  IP表第一个是58，表示明文的第58位被置换到第1位

• 轮结构：

  ​​

  • 明文中的64位数据分为L，R各32位。子密钥K为48位

  • 轮函数：

    • 将32位的R扩展为48位，才能和子密钥K进行异或
    • 由8个S盒子紧缩为32位
    • 经过P替换输出

  • 扩展函数E

    ​​

    • 通过上表，将32位的R变成48位

  • S盒代换操作：

    • 输入6位，输出4位表示一个十进制数（0~15）；第一位和第六位组成一个2进制数，选择行。其余位组成一个4位二进制数，选择列
    • ​​

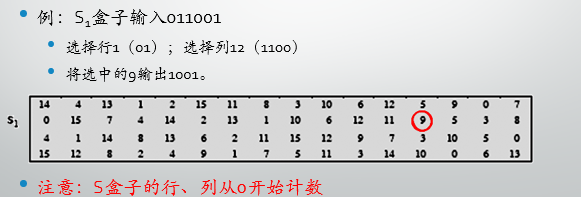
  • P盒置换操作：

    ‍

    ​​

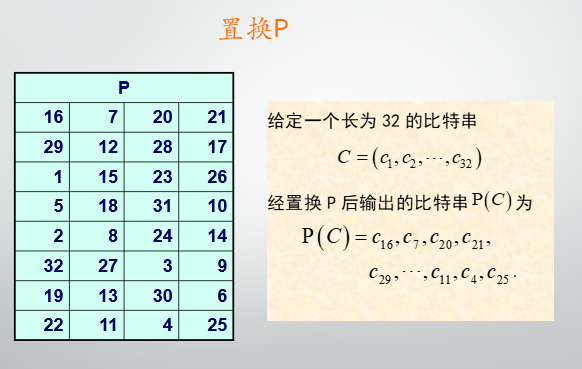
• 密钥编排算法：

  ​​

  ​​

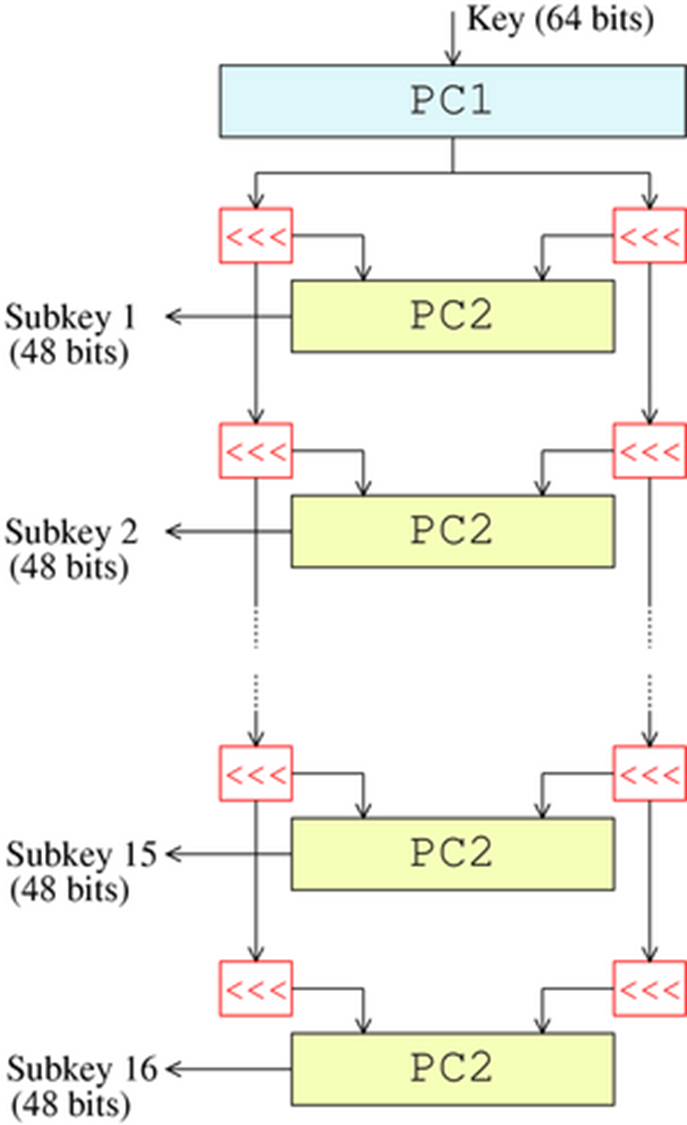
• 解密过程：加密和解密使用同一算法、同一密钥、同一结构。

• 安全性：

  • 期望的安全性

    • 密文的每个比特都依赖于密钥和明文的所有比特。
    • 改变任意单个明文比特或密钥比特都会使密文的每一个比特以1/2的概率改变。
    • 消除密文、明文、密钥之间的联系。

  • S盒的设计原则：

    • 每一行是0~15的置换
    • S盒的输出不是它的输入的线性或者仿射函数
    • 改变S盒的一个输入比特，其输出至少有2比特发生变化
    • $S(x) 与 S(x\oplus001100)$，至少2比特不同
    • $S(x) 与 S(x\oplus00xx00)$，至少2比特不同(x表示0/1)
    • 当任一输入位保持不变，其他5位输入发生变化时，输出的数字中的0和1的总数接近相等。

  • DES的密钥扩展算法有缺陷：DES的密钥扩展明显存在弱密钥和半弱密钥情形，这给安全性带来隐性威胁。

    ​​

  • 其他问题：

    • S盒设计可能有陷门；迭代次数少；软件实现慢；有效密钥位数少

• 现在一般用多重DES，最广泛的是三重DES

  • $DES-EEE_3$模式：使用三个不同密钥$(K_1,K_2,K_3)$ ，采用三次加密算法；

    $DES-EDE_3$模式：使用三个不同密钥$(K_1,K_2,K_3)$，采用加密一解密一加密算法；

    $DES-EEE_2$模式：使用两个不同密钥$(K_1=K_3,K_2)$ ，采用三次加密算法；

    $DES-EDE_2$模式：使用两个不同密钥$(K_1=K_3,K_2)$，采用加密一解密一加密算法。

国际数据加密算法IDEA

高级加密标准AES

分组密码操作模式

第四章

常用数学知识

群、环、域

• 半群：设$<G,>$是一个代数系统，$$满足封闭性，结合律

• 群：半群且有单位元（$ae=a$）和逆元​$(ax=e)$

• 有限群：G是有限的集合

• 群的阶数：G的元素个数

• 如果G中的$*$还满足交换律，那么这个群还可以称为交换群或者Abel群

• 循环群：设G为群，如果存在一个$g\in G$，满足$g^i$能表示$G$，则g称为循环群G的生成元。

  • 记：$G = $​
  • 称满足$a^m=e$的最小正整数m为a的阶

• 对于代数系统$<R,+,*>$满足：

  • $<R,+>$为交换群
  • $<R,*>$是半群
  • $*$对于+是可以分配的

  则称$R$为环

• 对于代数系统$<R,+,*>$满足：

  • $<R,+>$为交换群
  • $<R-{+的单位元},*>$是半群
  • $*$对于+是可以分配的

  则称R为域

素数和互素数

• $a|b$：a是b的因子，称为a整除b
• 任何一个数可以被分解为：$a=\prod_{p\in P}p^{a_p},a_p\ge 0$
• 互素数：$gcd(a,b)=1$，则a，b互质

模运算

• $a \bmod b = a-\lfloor \frac{a}{b} \rfloor *b$

• 如果$a\bmod n = b \bmod n$，则称a,b模n同余，记作$a \equiv b \pmod n$

• 乘法逆元：

  $ax \equiv 1 \pmod n$，则称x为a模n的乘法逆元

模指数定理

• 称满足$a^m \equiv 1 \pmod n$的最小正整数m为模n下a的阶，记为$ord_n(a)$
• $a^k \equiv 1 \pmod n$的充要条件是$k \bmod m = 0$

费马小定理，欧拉定理，卡米歇尔定理

• 费马小定理：

  $p \in prime,a \ge 0,\gcd(a,p)=1$，则$a^{p-1} \equiv 1 \pmod p$

• 欧拉定理：

  $a \ge 0,\gcd(a,p)=1$，则$a^{\phi(p)} \equiv 1 \pmod p$

  • $\phi(i)$为欧拉函数，意义为小于i的与i互质的数

    • $\phi(prime) = prime-1$
    • $\phi(n) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})…$,其中$p_i$为$n$唯一分解后的素因子

  • 推论：$ord_n(a) | \phi(n) $，如果二者相等，则称$a$为$n$的本原根

中国剩余定理

​​

​​

离散对数

• 对任意的$b\in {1,…,p-1}$，都存在唯一的$i(1 \le i \le p-1)$，使得$b \equiv a^i \bmod p$。则称$i$为模$p$下以$a$为底$ b$的指标，记为$i = ind_{a,p}(b)$。（假定$p$为素数，$a$为$ p$的本原根）

  • 性质1：$ind_{a,p}(1) = 0$
  • 性质2：$ind_{a,p}(a) = 1$

• 如果$a^z \equiv a^q \bmod p$，其中$p$为素数，$a$是$p$的本原根，则有$z \equiv q \bmod \phi(p)$

• $ind_{a,p}(xy) = [ind_{a,p}(x) + ind_{a,p}(y)] \bmod \phi(p)$

• $ind_{a,p}(y^r) = [r \times ind_{a,p}(y)] \bmod \phi(p)$

• 称上面的$i$为离散对数，记为$i \equiv log_a(b) \pmod p$

‍

公钥密码体制的基本概念

公钥密码体制原理

• 特点：采用两个相关密钥将加密和解密能力分开

  • 其中一个密钥是公开的，称为公开密钥，用于加密
  • 另一个密钥是为用户专用，因而是保密的，称为秘密密钥，用于解密

• 算法特性：已知密码算法和加密密钥，求解密密钥在计算上是不可行的。

• 公钥密码体制加密：

  ​​

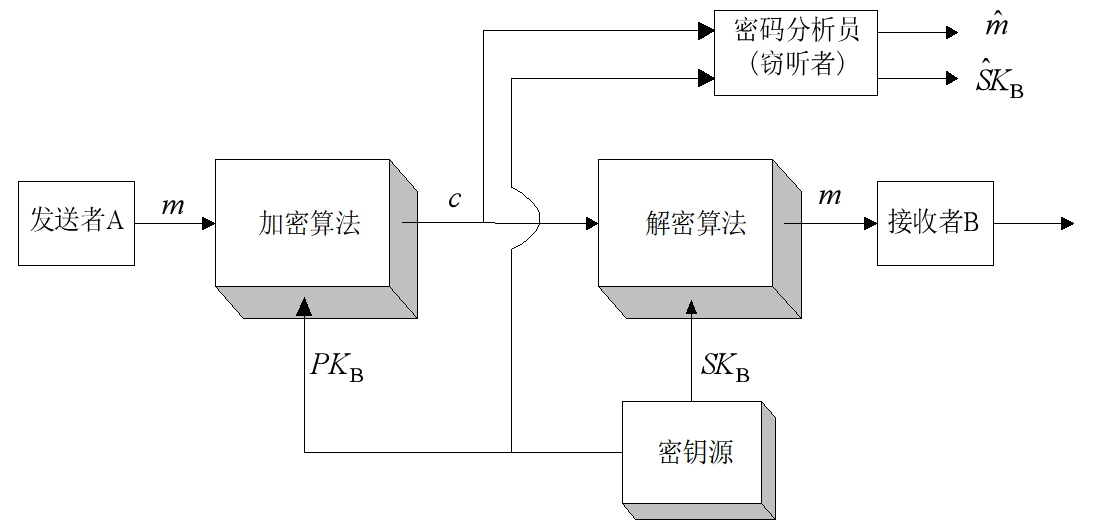
  • 接受者B需要产生一对密钥$PK_B,SK_B$。前者公开，后者保密
  • A发送信息的时候，$c = E_{PK_B}[m]$，$c $为密文，$E$为加密算法
  • B接受信息的是受，$m = \Delta_{SK_B}[c]$，$\Delta$是解密算法

• 公钥密码体制认证（可以对发送方A的信息m进行认证）：

  ​​

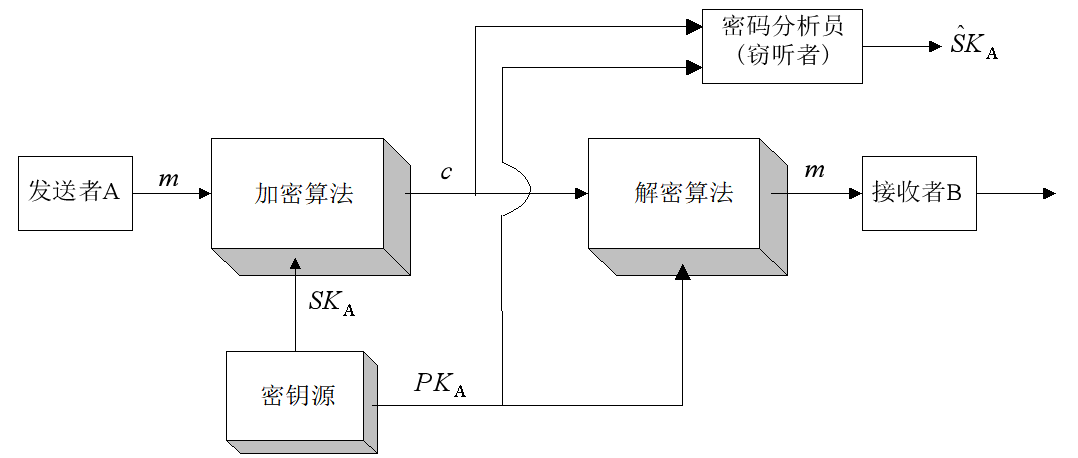
  • A用自己的私密钥$SK_A$对$m$加密，表示为$c = E_{SK_A}[m]$
  • 将$c$发到B。B用A的公开钥$PK_{A}$进行解密，$m = \Delta_{PK_{A}}[c]$
  • 因为从 $m$ 得到 $c$ 是经过 A 的秘密钥$SK_A$加密，只有A才能做到。因此 $c$ 可当做A对 $m$ 的数字签字。另一方面，任何人只要得不到A的秘密钥$SK_A$​就不能篡改 m ，所以以上过程获得了对消息来源和消息完整性的认证

• 认证符：

  • 上面的认证方法需要很大的存储空间，需要减小文件的数字签字的大小，即将文件经过一个函数压缩成长度较小的比特串，得到的比特串称为认证符。
  • 加密过程为：$c = E_{PK_B}[E_{SK_A}[m]]$​
  • 解密过程为：$m = \Delta_{PK_A}[\Delta_{SK_B}[c]]$
  • 同时提供认证功能和保密性

  ​​

‍

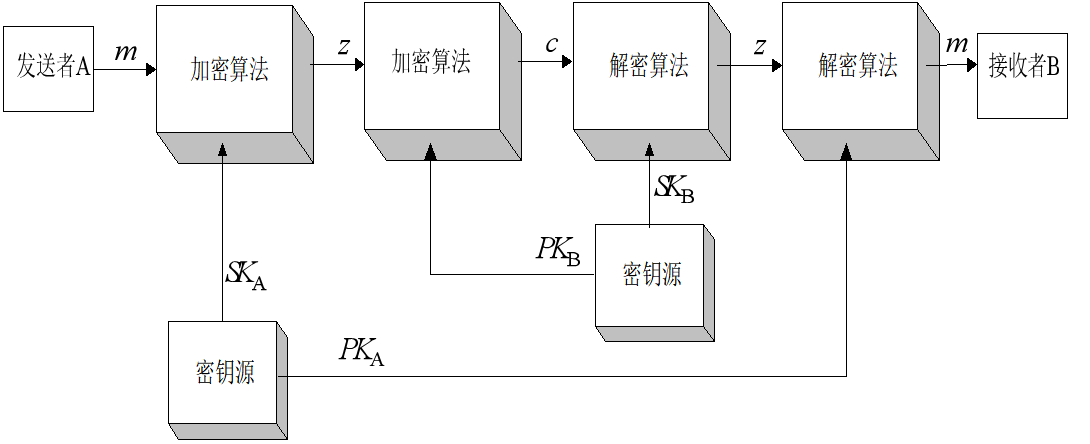
公钥密码体制应满足的要求

• 密钥对的产生，加密，解密过程是计算上容易的
• 由公开钥求私密钥是计算上不可行的
• 由密文和公开钥来恢复明文是计算上不可行的
• 加解密次序可换（不做强制要求）

​​

对公钥密码体制的攻击

• 穷举：密钥太短，也会被穷举攻击破解。但是密钥太长，复杂度会增长的很快

• 可能字攻击（仅适用于对公钥密码算法）：

  • 例如对56比特的DES密钥用公钥密码算法加密后发送，敌手用算法的公开钥对所有可能的密钥加密后与截获的密文相比较。
  • 如果一样，则相应的明文即DES密钥就被找出。因此不管公钥算法的密钥多长，这种攻击的本质是对56比特DES密钥的穷搜索攻击
  • 抵抗方法是在欲发送的明文消息后填加一些随机比特。

• 公钥密码体制目前主要用于密钥管理和数字签字。

RSA算法

算法描述

• 密钥的产生

  1. 选择两个保密的大素数$p$和$q$
  2. 计算$n = p \times q,\phi(n) = (p-1)(q-1)$
  3. 选择一个整数$e$，满足$1 <e<\phi(n)$，并且$\gcd(\phi(n),e) = 1$
  4. 计算$d$，满足$d \times e \equiv 1 \bmod \phi(n)$（即$d$是$e$在模$\phi(n)$的乘法逆元）
  5. 公开钥为${n,e}$，私密钥为${n,d}$

• 加密：

  加密时首先将明文比特串分组，使得每个分组对应的十进制数小于$n$，即分组长度小于$log_2n$，然后对每个明文分组$m$，加密：$c \equiv m^e \bmod n$

• 解密 $m = c^d \bmod n$

• ​​

计算问题

• 边乘边取模
• 快速幂

改进方法

​​

安全性

• 安全性是基于分解大整数的困难性假定，之所以为假定是因为至今还未能证明分解大整数就是 NP 问题，也许有尚未发现的多项式时间分解算法。
• 即如果RSA的模数$n$被分解为$p \times q$，那么就可以直接确定$\phi(n)$，由此确定$d,e $

对RSA的攻击

RSA存在以下两种攻击，并不是因为算法本身存在缺陷，而是由于参数选择不当造成的。

1. 共模攻击

• 不能为每一个用户相同的模数$n$，不然会有问题